In this course we build and define basic structures that rely on sets and binary operations. We start with systems, defined with one binary operation and move on to systems with two binary operations. The course will be taking a formal approach containing definitions, theorems, lemmas and proofs. Examples will be interspersed throughout.

In this course we take an axiomatic approach in defining a vector space. Functions on vector spaces are then defined. Various other spaces are defined such as innerproducts and eigenspaces. The course will be take a formal approach, containing definitions, theorems, lemmas and proofs. Examples will be interspersed throughout.

This is a classical course in the theory of probability - the branch of mathematics that quantifies uncertainty. The course provides an initial review of concepts in elementary probability, before moving to a detailed exploration of the notions of density, distribution and moment for discrete and continuous random variables. Various case study examples are used to show how these ideas can be used in solving real-world problems.

Multivariable Calculus applies the techniques and theory of differentiation and integration to vector-valued functions and functions of more than one variable. The course presents a thorough study of vectors in two and three dimensions, vector-valued functions, curves and surfaces, motion in two and three dimensions, and an introduction to vector fields. Students will be exposed to modern mathematical software to visually represent these 2D and 3D objects.

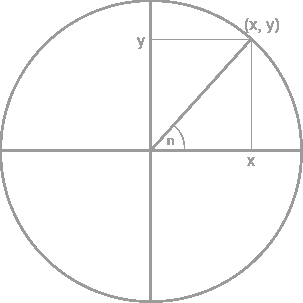
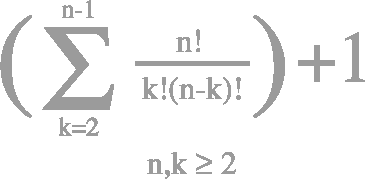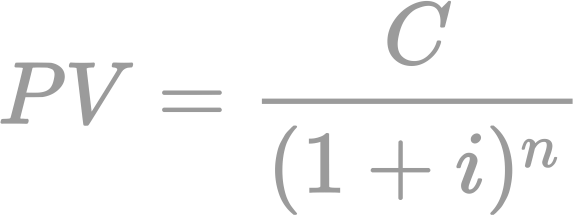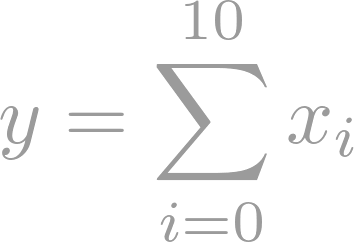This is a classical course in analysis, providing a foundation for many other mathematical courses. The course exposes students to rigorous mathematical definitions of limits of sequences of numbers and functions, classical results about continuity and differentiability, series of numbers and functions, and their proofs. A particular focus of the course is in providing students with practical expertise working with rigorous definitions and creating proofs. The following topics will be covered: sequences, continuity, differentiability, series of numbers, series of functions.

Ordinary differential equations; Laplace transform; Fourier series; Partial differential equations; Vector calculus; Line integrals; surface integral Stroke theorem and divergence theorem.