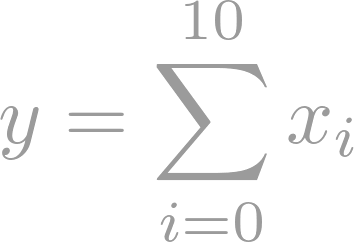
At present the most developed part of the research activity of the Department of Mathematics can be characterized as Pure Mathematics, Applied Mathematics, Statistical Sciences, Actuarial Science and Financial Mathematics. Following are the list of the researchers and their area of interests of our department.
Recently, the Department of Mathematics begun to be involved into the research in the area of Mathematical Education and we will update the information here soon.
|
Name of the Faculty Members |
Research Interests |
| Dr. Nagarani Ponakala | Physiological Fluid Dynamics, Non-Newtonian Fluids, Computational Methods, Non-linear Differential Equations, Special Functions and Applications. |
| Dr. Mahesha Narayana | Computational Methods, Fluid Mechanics. |
| Longitudinal Data Analysis, Early Life Predictors of Cardiovascular Disease, Factor Analysis, Principal Component Analysis, Survival Analysis. | |
| Dr. Diptiranjan Behera | Fuzzy and Interval Mathematics, Computational Methods, Fractional Differential Equations, Non-Linear Differential Equations, Structural Analysis, Optimization Problems. |
| Dr. Kirk Morgan | Stochastic Difference Equations, General Relativity. |
| Mr. Ajani Ausaru | Biomechanics |
| Mr. Howard Hines | Reduction of Climate Risks to Industry and Livelihoods, Research on Health Insurance |
| Dr. Nordia Thomas | Market Microstructure, Fintech, Financial taxation, Financial Regulation. |
| Mr. W. St. Elmo Whyte | Stochastic Processes, Enterprise Risk Management |
| Prof. Alexandra Rodkina | Asymptotic Behavior of Solutions of Nonlinear Stochastic Functional-Differential and Difference Equations, Stability of Numerical Methods for Nonlinear Stochastic Equations, Applications in Mechanics, Engineering, Mathematics of Finance, Risk Theory. |
Explanation of some of the active research areas in the department are as follows.
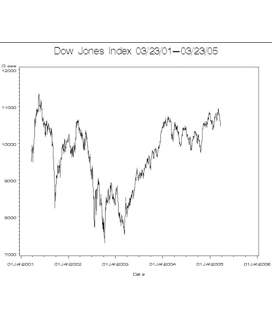
Stochastic equations are used to model real-world systems that are subject to interference in the form of randomexternal perturbations or feedback noise. This interference can have a dramatic qualitative effect on these systems and should therefore be included in any analysis of their behaviour. For example population models may be designedto reflect the unpredictable effects of disease and environment, as well as classical predator-prey, birth-death dynamics.
Our 7 faculties and 12 professional schools offer more than 200 programmes to some 18,000 graduate, undergraduate and continuing studies students.
The UWI, Mona ranks first in Jamaica among accredited tertiary-level programmes. In 2012, the University was again one of Jamaica’s Top 100 Employers.
