Each student will work on a mathematical project under the supervision of a faculty member. The project will culminate in an oral presentation to the Department of Mathematics. The topic of the project will agreed upon by the student and supervisor.

This course examines metric and topological spaces, continuity, completeness, and compactness, providing a theoretical foundation for further work in differential equations, probability theory, stochastic processes, differential geometry and mathematical physics.

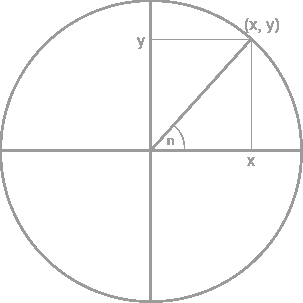
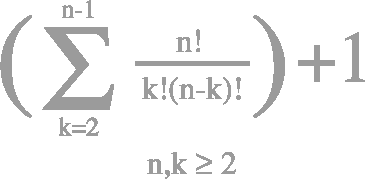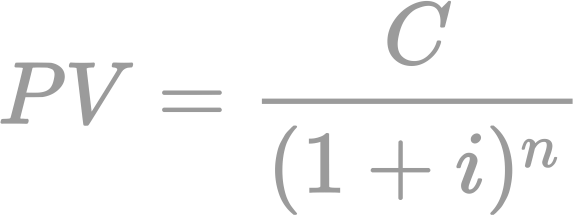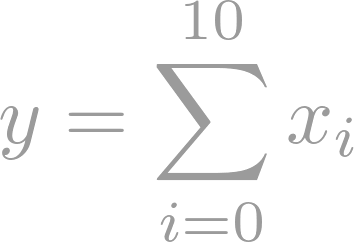The course develops the properties of the complex number system, treated as a generalisation of the real number system. We explore the parallel analysis that results, with a particular emphasis on differentiability, analyticity, contour integrals, Cauchy’s  theorem, Laurent series representation, and residue calculus.

This course considers the limitations of the Riemann integral, and shows that it it necessary to develop a precise mathematical notion of ‘length’ and ‘area’ in order to overcome them. Thus we develop the concept of measure, and use it to construct the more powerful Lebesgue integral, and explore its properties. Finally we look at applications of measure and Lebesgue integration in modern probability theory.

Functional analysis is mainly concerned with the study of vector spaces and operators acting upon them. It provides powerful tools in handling several problems in applied mathematics and theoretical physics. It is also basic for the understanding and development of very many other mathematical theories like the Theory of Partial Differential Equations and the Theory of Operators.