





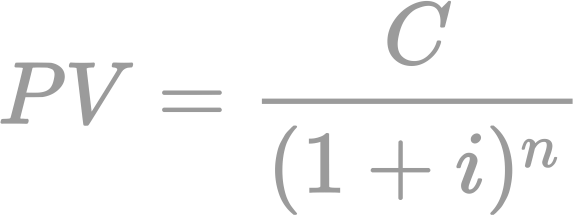
Course Code: MATH 2401 |
Level: II |
No. of Credits: 3 |
Prerequisites: (MATH1141, MATH1142, MATH1151 and MATH1152) or (M10A, M10B) |
Course Description: This is a classical course in analysis, providing a foundation for many other mathematical courses. The course exposes students to rigorous mathematical definitions of limits of sequences of numbers and functions, classical results about continuity and differentiability, series of numbers and functions, and their proofs. A particular focus of the course is in providing students with practical expertise working with rigorous definitions and creating proofs. The following topics will be covered: sequences, continuity, differentiability, series of numbers, series of functions. |
Content: Sequences; Limits and Continuity; Differentiability; Infinite Series; Sequence and Series of functions. |
Assessment: The course assessment has three components consisting of a final exam worth 70%; two midterm Exams worth 10% each; and two written assignments 5% each. |
Course Code: MATH 2403 |
Level: II |
No. of Credits: 3 |
Prerequisites: (MATH1141, MATH1142 and MATH1151) or (MATH1185) or (M10A and M10B) |
Course Description: Multivariable Calculus applies the techniques and theory of differentiation and integration to vector-valued functions and functions of more than one variable. The course presents a thorough study of vectors in two and three dimensions, vector-valued functions, curves and surfaces, motion in two and three dimensions, and an introduction to vector fields. Students will be exposed to modern mathematical software to visually represent these 2D and 3D objects. |
Content: Parametric and polar curves; vectors and vector-valued functions; functions of several variables; multiple integration; vector calculus. |
Assessment: The course assessment will be broken into two components; a coursework component consisting of two course work exams and each of these exams will be worth 15% of the student’s final grade and and a final exam worth 70%. |
Course Code: MATH 2420 |
Level: II |
No. of Credits: 3 |
Prerequisites: (MATH 1141, MATH 1142, MATH 1151 & MATH 1151) or (M10A & |
Course Description: This is a Level II compulsory course for majors and minors in Mathematics, which is suitable for all science students. This course introduces methods for solving first- and second-order ordinary differential equations, systems of differential equations, and power series solutions. The purpose of this course is to introduce students to the theory and application of differential equations. Specifically, the course prepares students to apply differential equations to scientific, engineering and economic problems. Furthermore, students will be exposed to modern mathematical software (Math Lab or Maple) to explore the concepts encountered in the course. |
Content: Classification of Differential Equations; First Order Differential Equations; Higher Order Linear Equations; Power series solutions; Legendre polynomials and Bessel functions |
Assessment: The course assessment will be divided into two components: a coursework component worth a 30% and a final exam worth a 70%.
Two one-hour course work exams will take place during weeks 5 and 9. Each will be worth a 10% of the student’s final grade.
Written assignments (problem papers), total grade worth a 10% of the student’s final grade.
The final theory exam will be two hours in length and consist of compulsory questions. |
Course Code: MATH 2421 |
Level: II |
No. of Credits: 3 |
Prerequisites: (MATH1141, MATH1142 & MATH1151) or (MATH1185) or (M10A & M10B) |
Course Description: The course introduces mathematical techniques commonly used in mathematical modeling, and demonstrates their application to problems in physics and engineering. The course requires students to actively apply these techniques in similar problems. |
Content: Fourier Series; Laplace Transforms; Fourier Transforms; Special functions. |
Assessment: The course assessment will be broken into two components; a coursework component consisting of two mid semester exams worth 10% each and five take home assignments worth 4% each and a final theory exam worth 60%. |
Course Code: MATH 2430 |
Level: II |
No. of Credits: 3 |
Prerequisites: (MATH1141 & MATH1152) or (M10A & M10B) |
Course Description: The purpose of this course is to introduce students to the methods and techniques of some key areas of mathematical models in Operations Research. This course analyzes the mathematical modeling that can be applied in solving the problems in industry, business, science and technology, management, decision support and other areas and disciplines. |
Content: inear programming Introduction and formulation; Graphical Method; Simplex Method; Big M Method; Two Phase Method; Duality; Sensitivity Analysis |
Assessment: The course assessment will be broken into two components; a coursework component consisting of two mid semester exams worth 15% each and a final exam worth 70%. |
Course Code: MATH 2431 |
Level: II |
No. of Credits: 3 |
Prerequisites: (MATH 1141 & MATH 1142) or (M10A & M10B) |
Course Description: In this course students will be introduced to different forms of optimization problems and the various approaches that are available to solve such problems. The course will conclude with defining and solving non-linear programming problems. The course contains numerous definitions, theorems, lemmas and proofs. Examples will be interspersed throughout. |
Content: Optimization of functions of several variables; Non-linear programming problems |
Assessment: The course assessment will have a course-work component consisting of a mid semester exam worth 20% and two take home graded assignments (problem papers) worth 5% each; and a final theory exam worth 70%. |
Course Code: MATH 2701 |
Level: II |
No. of Credits: 3 |
Prerequisites: (MATH1141, MATH1142, MATH1151 & MATH1152) or (M10A & M10B). |
Course Description: This is a compulsory level II course which is an important foundation course in actuarial science and finance. Candidates should master the fundamental concepts of financial mathematics and its simple applications. This course allows the candidate to begin preparation for the professional Financial Mathematics examinations (the Society of Actuaries course FM and the faculty/Institute of Actuaries CT1 exam) as well as the Quantitative Methods section of the CFA level I exam. |
Content: Basic interest theory; Time value of money; General cash flow & portfolios; Annuities with non-contingent payments; Basic applications |
Assessment: The course assessment will be divided into two components: a coursework component consisting of two written assignments worth 5% each and a mid semester exam worth 15%; and a final exam worth 75%. |
Course Code: MATH 2702 |
Level: II |
No. of Credits: 3 |
Prerequisites: MATH2701 and MATH2404 |
Course Description: This is a compulsory level II course which is an important foundation course in actuarial science. Candidates should master the fundamental concepts of actuarial and financial mathematics and its simple applications. This course allows the candidate to begin preparation for the professional examinations (the Society of Actuaries Actuarial Models examination, Exam 3 of the Casualty Actuarial Society, and the Faculty/Institute of Actuaries Contingencies examination). It covers practical applications such as the computational aspects of pricing and prepares the candidate for the follow up courses in reserving and risk measurement of insurance portfolios. The course contains survival distributions and life tables – applications of probability to problems of life and death, the determination of premiums for insurances and annuities in both the discrete and continuous cases and net Premiums. |
Content: Survival models; Life Insurances and Annuities; Premiums |
Assessment: The course assessment will be divided into two components: a coursework component consisting of a mid semester exam worth 15% and two written assignments (problem papers) worth 5% each; and a final exam worth 75%: |
Course Code: MATH1141 |
Level: Undergraduate |
No. of Credits: 3 |
Prerequisites: CAPE Pure Mathematics, Units 1 & 2, GCE A-Level Mathematics or MATH0100 and MATH0110 or its equivalent |
Course Description: COURSE NAME AND CODE: Introductory Linear Algebra and Analytic Geometry (MATH 1141) SEMESTER: I NUMBER OF CREDITS: 3 COURSE DESCRIPTION: CONTENT: OBJECTIVES: At the end of the course, students will be able to:
Definition, inverse function, graphs of some elementary functions and elementary transformations of the graphs. Lab : [10 hours] Problem solving and simulations. TEACHING METHODOLOGY Online Resources: |
Content: |
Assessment: |
Course Code: MATH2230 |
Level: II |
No. of Credits: 3 |
Prerequisites: MATH1180 |
Course Description: Ordinary differential equations; Laplace transform; Fourier series; Partial differential equations; Vector calculus; Line integrals; surface integral Stroke theorem and divergence theorem. |
Content: |
Assessment: The course assessment has two components consisting of one 2 hour paper worth 75% and two mid semester exams worth 25%
This course is designed for students majoring in Electronics Engineering only. |
Course Code: MATH2404 |
Level: II |
No. of Credits: 3 |
Prerequisites: (MATH1141, MATH1142, MATH1151 & MATH1152) or (M10A & M10B) |
Course Description: This is a classical course in the theory of probability - the branch of mathematics that quantifies uncertainty. The course provides an initial review of concepts in elementary probability, before moving to a detailed exploration of the notions of density, distribution and moment for discrete and continuous random variables. Various case study examples are used to show how these ideas can be used in solving real-world problems. Finally, asymptotic theory is presented, with an illustration of the use of the Weak Law of Large Numbers and the central limit theorem in sampling technique and approximation. |
Content: Review of basic notions of probability; Discrete random variables; Continuous random variables; Asymptotic theory. |
Assessment: The course assessment has three components consisting of an in-course test worth 15%; two assignments worth 7.5% each and a final exam worth 70%. |
Course Code: MATH2410 |
Level: II |
No. of Credits: 3 |
Prerequisites: (MATH 1141 & MATH 1152) or (M10A & M10B) |
Course Description: In this course we take an axiomatic approach in defining a vector space. Functions on vector spaces are then defined. Various other spaces are defined such as innerproducts and eigenspaces. The course will be take a formal approach, containing definitions, theorems, lemmas and proofs. Examples will be interspersed throughout. |
Content: Properties of Matrices and Determinants; Vector spaces; Linear transformations; Inner products; Eigenspaces. |
Assessment: The course assessment will have a course-work component consisting of one in-mid-semester examination worth 20% and two take-home graded assignments (problem papers) worth 5% each; and a final exam worth 70%. |
Course Code: STAT 2001 |
Level: II |
No. of Credits: 3 |
Prerequisites: STAT1001 or MATH2104 |
Course Description: In this course, we take a more fundamental approach to estimation and quantifying the accuracy of estimates. There will also be some graphical interpretation with some examples and exercises making use of the statistical computer package R. In statistical inference, we use a sample of data to draw inferences about some aspect of the population (real or hypothetical) from which the data were taken. Often the inference concerns the value of one or more unknown parameters, which describe some attribute of the population such as its location or spread. There are three main types of inference, namely, point estimation, interval estimation and hypothesis testing. |
Content: Sampling Distribution, Parameter Estimation, Interval Estimation, Hypothesis Testing, Goodness-of-fit test |
Assessment: The course assessment entails a course- work component consisting of a mid semester exam with 15% and a problem paper/lab assignment worth 15%; and a final theory exam worth 70%. |
Course Code: STAT 2002 |
Level: II |
No. of Credits: 3 |
Prerequisites: STAT1001: Statistics for the Sciences, MATH1142: Calculus I |
Course Description: This course will enable the students to perform a range of nonparametric methods and robust procedures that do not assume that the sample data are from pre-specified families of distribution. We will first look at the definition of scales of measurement, the pros and cons for weak assumptions, test of locations and other distribution-free methods. This will prepare students who are interested in research (qualitative and quantitative), socio-economic and environmental problems, and ratings (movie, celebrities etc.) to name a few. |
Content: Introduction: Scales of Measurements; Inference on Location: Inference on Dispersion; Rank Correlation; Test of Randomness; Goodness of Fit; Design of Experiment; Categorical Data |
Assessment: The Course will be assessed as follows:
i. Mid-term test worth 15%
ii. Problem Papers/Lab assignments 15%
iii. Final written examination paper worth 70% |
Course Code: STAT2003 |
Level: II |
No. of Credits: 3 |
Prerequisites: STAT1001: Statistics for the Science, STAT2001: Inferential Statistics |
Course Description: The course will consist of a mixture of lectures and practical work (which will be assessed by the student’s completion of practical assignments to be submitted); Computer practical sessions in which the statistical package R, will be used to analyse the data. This will be the basis on which continuous assessment will be conducted. The lectures will focus on statistical modelling, including selection of appropriate models, the analysis and interpretation of results and diagnostics. Exploratory and graphical techniques will be considered, as well as formal statistical procedures. Practical applications will be emphasised throughout. |
Content: Exploratory Data Analysis; Linear Regression; Logistic Regression; Analysis of Variance:
|
Assessment: This course assessment is 100% coursework. The coursework elements are as follows:
Project 1 40%
Project 2 40%
Problem papers (about 2) 20% |