This course develops Complex Analysis as an extension of Real Analysis. Apart from concentrating  on the theoretical developments, emphasis will be on unifying aspects in theory and applications. Examples will be taken from different applied subjects to showcase the elegance and utility of introducing methods based on complex analysis.

This course is about the analysis of manifolds such as curves, surfaces and hypersurfaces in higher dimensional space using the tools of calculus and linear algebra. There will be many examples discussed, including some which arise in the theory of general relativity. Emphasis will be placed on developing intuitions and learning to use calculations to verify and prove theorems. Students need a good background in linear algebra. Some exposure to differential equations is helpful but not absolutely necessary.

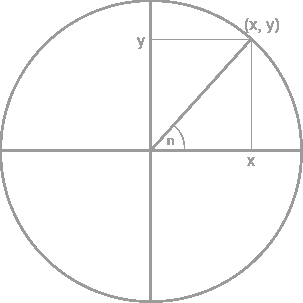
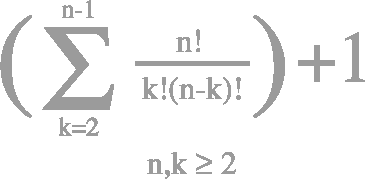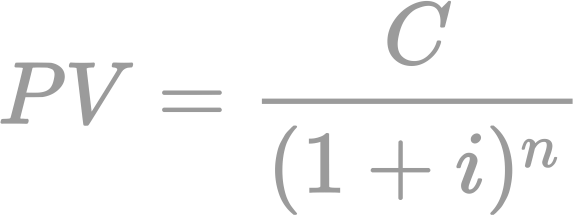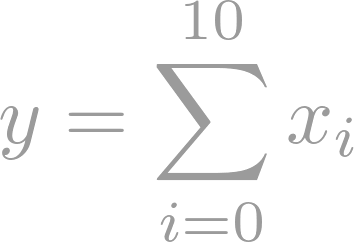In this course, students will study the origins and development of topics of great modern importance. The course is designed primarily for graduate students interested in teaching and mathematics pedagogy. However, it is suitable for all mathematics students also. The course will focus primarily on the axiomatic development of mathematics, the creative processes leading to new methods, and, the development of the calculus.

The aim of the course is to teach students the tools of modern algebra and number theory as it is related to further study in mathematics. This course is intended to develop the ability of the students to work with abstract ideas and their applications.

The course gives an up-to-date and modern overview of the main concepts in the Mechanics of interacting particles. Starting with an introduction to Newtonian mechanics and the Lagrangian/Hamiltonian formalism the course continues with an axiomatic approach to Quantum Mechanics. Path integrals and path integral quantization of Bosonic and Fermionic particles are also treated. A short introduction to Gauge Theories and the Higgs field is given at the end of the course.

The course gives an up-to-date and modern overview of the main concepts in Group Theory. Group theoretical properties and several examples of groups arising in many branches of mathematics, physics, and chemistry are studied to show how group theory emerges in different mathematical fields and in applied sciences.

The course covers the fundamental concepts required for the description, modeling and forecasting of time series data, both in the time- and frequency-domains. Attention to the theoretical underpinnings of the subject is complemented by the analysis of real-world data sets, and a practical laboratory component introduces students to the software package R.

The course covers the fundamental concepts required for the description, modeling and forecasting of time series data, both in the time- and frequency-domains. Attention to the theoretical underpinnings of the subject is complemented by the analysis of real-world data sets, and a practical laboratory component introduces students to the software package R.

This course aims to give students a broad overview of the main concepts in the theory of probability and stochastic processes. It will provide students with solid grounding in modern probabilistic and statistical methods.