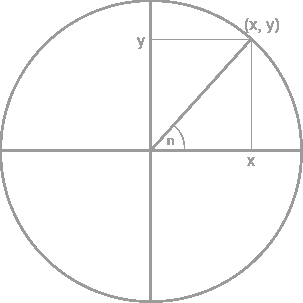
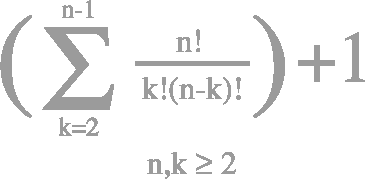
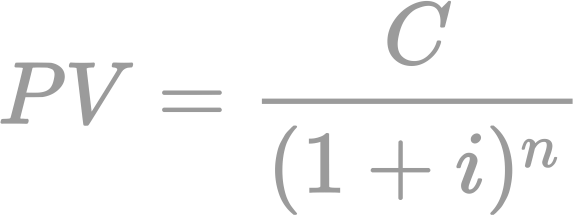
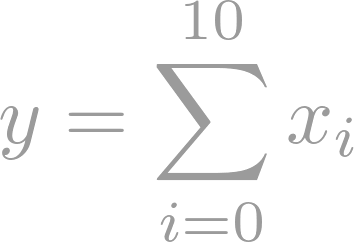
Topology is the study of spaces and sets and can be thought of as an extension of geometry. It is an investigation of both the local and the global structure of a space or set. The foundation of General Topology (or Point-Set Topology) is set theory.  The motivation behind topology is that some geometric problems do not depend on the exact shape of an object but on the way the object is put together. The course gives an up-to-date and modern overview of the main concepts in General Topology. Topological properties and several examples of topological spaces arising in several branches of mathematics are studied to show how topology is a unifying theme in different mathematical fields.  A course in general topology is essential for enrolled students since it provides them with fundamental notions such as those of topological space, topological vector space, connectedness, and compactness.